| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Bounding box regressor
- Multi-task loss
- Non maximum suppression
- YOLO
- detr
- RoI pooling
- RPN
- Anchor box
- mean Average Precision
- IOU
- object queries
- fine tune AlexNet
- hard negative mining
- Fast R-CNN
- Faster R-CNN
- Linear SVM
- herbwood
- Region proposal Network
- Detection Transformer
- Object Detection
- Map
- BiFPN
- Average Precision
- multi task loss
- pytorch
- AP
- Object Detection metric
- Hungarian algorithm
- Darknet
- R-CNN
- Today
- Total
약초의 숲으로 놀러오세요
Object Detection의 정의와 Metric mAP(mean Average Precision) 본문
Object Detection의 정의와 Metric mAP(mean Average Precision)
herbwood 2020. 11. 13. 23:18최근 컴퓨터 비전 분야에서는 이미지를 분류하는 것을 넘어 이미지에 존재하는 사물을 검출하는 Object detection에 대한 연구가 활발히 진행되고 있습니다. Object detection은 자율 주행차, 얼굴 및 보행자 검출, 영상 복구, OCR, Vision Inspection 등 다양한 분야에서 활용되고 있습니다. 저도 Object detection에 관심을 가져 관련 논문을 읽어보고자 했으나, 이미지 분류와는 다른 문제 정의, 모델 구조, 그리고 평가 방식의 차이를 이해하지 못해 좌절했습니다😂 그래서 관련 논문을 본격적으로 살펴보기에 앞서 Object detection의 정의와 평가 방법에 대해 공부한 내용을 정리해보았습니다.
Object Detection의 정의

- Image Classification = (single object)Classification
- Image Localization = (single object)Localization
- Object Detection = (multi objects)Localization + (multi objects)Classification
컴퓨터 비전 분야에서의 과제는 이미지 내 존재하는 객체의 수와 객체의 위치 판별 여부에 따라 다르게 정의할 수 있습니다. 우리에게 익숙한 Image Classification은 이미지 내 존재하는 단일 객체에 대한 범주(class)를 예측하는 문제입니다. Image Localization은 이미지 내 존재하는 단일 객체의 위치를 Bounding Box라고 불리는 사각형을 통해 예측하는 문제입니다. 이에 더하여 Object Detection은 이미지 내 존재하는 다수의 객체에 대한 위치를 예측하는 동시에 해당 객체에 대한 범주를 예측하는 문제입니다.

이러한 작업을 수행하는 Object Detection 모델은 이미지를 입력으로 받아 이미지 내 존재하는 객체의 위치와 객체의 범주(class)를 예측합니다. 더 구체적으로 보면, 모델은 Bounding box의 좌표값과 Confidence score를 반환합니다.
- Bounding box는 이미지 내에서 객체의 위치를 사각형 형태로 예측한 결과로, 모델은 사각형의 좌상단 좌표(x1, y1)과 우하단 좌표(x2, y2) 좌표를 반환합니다. 사각형의 좌표 형식은 모델마다 조금 상이합니다.
- Confidence score는 예측한 box 내 존재하는 객체의 범주를 예측한 확률의 최대값입니다. 예를 들어 위의 그림을 보면 Confidence score가 0.8이라는 것은 모델이 생성한 bounding box 내의 객체가 오리너구리일 확률이 80%라고 확신한다고 생각하면 쉽습니다.
모델은 이미지 내에서 다수의 Bounding box를 예측하며, 예측한 box마다 confidence score를 가집니다. 이같은 모델의 정확도를 평가하기 위해 먼저 객체 위치의 정확도를 평가하는 지표인 IoU를 살펴보도록 하겠습니다.
Object Detection Metric
1) IoU(Intersection over Union)

IoU(Intersection over Union)는 객체의 위치 추정의 정확도를 평가하는 지표입니다. 실제 객체의 위치인 bounding box를 $B_{gt}$(ground truth)라고 하고, 예측한 bounding box를 $B_p$(predicted)라고 할 때 두 box가 겹치는 영역의 크기를 통해 평가하는 방식입니다. 두 box가 겹쳐지는 영역이 넓다는 것은 모델이 객체의 위치를 잘 추정했다는 것을 의미합니다. IoU는 0과 1 사이의 값을 가집니다. PASCAL VOC 데이터셋에서는 IoU가 0.5 이상일 경우(객체의 예측 위치가 실제 위치와 절반 이상 겹칠 경우), 올바르게 예측했다고 간주합니다. 즉 모델이 예측한 이미지 내 Bounding box 별로 IoU를 구해 위치 추정의 정확도를 구할 수 있습니다.
2) Precision and Recall basic
Object Detection 모델을 평가하기 위해 앞서 살펴본 IoU를 기반으로 Precision과 Recall 지표를 구합니다. 이를 본격적으로 살펴보기에 앞서 Precision과 Recall에 대해 살펴보도록 하겠습니다(매번 접하지만 볼때마다 기억이 안나서 제대로 정리합니다😤).
Precision(정밀도)은 모델이 예측을 양성(positive)으로 한 대상 중에 예측과 실제 값이 양성으로 일치한 데이터의 비율을 의미하며 Recall(재현율)은 실제 값이 양성(positive)인 대상 중에서 예측과 실제 값이 양성으로 일치한 데이터의 비율을 뜻합니다. Precision과 Recall 값은 오차행렬(Confusion Matrix)를 통해 쉽게 파악할 수 있습니다.

$$Precision = {TP \over TP + FP}$$
$$Recall = {TP \over TP + FN}$$
오차 행렬을 보면 실제 범주(Actual Class)와 예측 범주(Predicted Class) 사이의 관계를 도표로 잘 드러냅니다. Confusion Matrix 왼쪽에는 제가 매번 공부할 때마다 헷갈려서 저만의 이해 방식을 적어봤습니다🤣. 위의 수식에서 볼 수 있듯이 Precision은 예측한 양성 중(TP + FP)에 실제 양성(TP)의 비율을 의미하며, Recall은 실제 양성(TP + FN) 중에 예측한 양성(TP)입니다.
3) IoU 임계값과 Confidence score 임계값
Object Detection 문제에서 실제 양성(positive)은 Ground truth box이며, 예측한 결과는 모델이 생성한 예측 bounding box입니다. 예측 bounding box의 양성 여부, 즉 객체의 위치를 성공적으로 포착했는지 여부는 IoU 임계값(Threshold)을 기준으로 정합니다. IoU 임계값이 0.5인 경우(ground truth box와 절반 이상 겹칠 경우), 이보다 작은 IoU를 가지는 bounding box는 음성(negative)로 봅니다. 아래 사진을 보고 더 자세히 설명하도록 하겠습니다.

위의 그림에서 녹색 box는 실제 객체의 위치인 ground truth box이며, 빨간 box는 모델이 예측한 bounding box입니다. 각 Bounding box별로 인덱스(박스 번호), 객체의 범주, confidence score가 매겨진 것을 확인할 수 있습니다. IoU 임계값을 0.5라고 할 때,
- 1, 4, 5번 bounding box는 ground truth box와 절반 이상 겹치므로 실제 객체의 위치를 올바르게 검출한 TP(True Positive)에 해당합니다.
- 2, 3번 box는 객체의 위치를 예측했지만 IoU가 0.5 미만이므로 FP(False Positive)에 해당합니다. 특히 3번 box의 경우, 객체와 겹치는 부분이 아예 없습니다.
- 마지막으로 가운데 있는 강아지는 검출되어야 했지만 검출되지 못한 사례로 FN(False Negative)에 해당합니다. 모델이 객체가 없다고 판단했지만 실제로 객체가 존재했기 때문입니다.
- TN(True Positive)같은 경우 Object Detection 모델은 실제 객체의 위치를 찾는 모델이기 때문에 객체가 없는 경우를 별도로 검출하지 않기 때문에 사용하지 않습니다.
위의 그림에서 예측한 bounding box의 수(FP + TP)는 5개이며, 실제 객체가 존재하는 ground truth box의 수는 5개입니다. TP=3이므로, Precision(=TP/(FP+TP))=3/5=0.6이며, Recall=(=TP/(FN+TP))=3/5=0.6입니다.

IoU의 임계값이 높아지면 그만큼 TP에 해당하는 box의 수가 줄고 FP에 해당하는 경우의 수가 늘어날 것입니다. IoU 임계값뿐만 아니라 confidence score 임계값(threshold)에 따라 Precision과 Recall 값이 달라질 수 있습니다. confidence score는 앞서 살펴본 바와 같이 모델이 검출한 객체가 특정 범주에 속할 확률이 얼마나 확실한지를 나타내는 지표입니다. 따라서 confidence score에 적절한 임계값을 두면 객체 검출의 정확도가 낮은 bounding box는 검출 실패로 볼 수 있습니다. 강아지 그림에서 confidence score 임계값을 조정하면 위의 그림과 같이 Precision과 Recall값이 변화하는 것을 확인할 수 있습니다.
Confidence score의 임계값이 낮을수록 더 많은 bounding box를 생성하기 때문에 Recall 값은 높아지나, Precision 값은 낮아집니다. 반대의 경우 bounding box를 만드는데 매우 신중하게 되기 때문에 Precision 값은 높아지나, Recall 값이 낮아집니다. 이처럼 Precision과 Recall은 서로 반비례 관계를 가지고 있습니다. Precision과 Recall은 상호 보완적인 평가 지표이기 때문에 어느 한쪽을 강제로 높이면 다른 쪽의 수치는 떨어지기 쉽습니다. 이를 Precision/Recall 트레이드오프(Trade-off)라고 부릅니다.
5) AP(Average Precision)
Recall 값의 변화에 따른(confidence score 값을 조정하면서 얻어진) Precision값을 나타낸 곡선을 PR 곡선(Precision-Recall Curve)이라고 합니다. 그리고 이렇게 얻어진 Precision 값의 평균을 AP(Average Precision)라고 하며, 일반적으로 PR 곡선의 면적(AUC, Area Under Curve)값으로 계산됩니다. AP는 Precision과 Recall을 모두 고려하여 얻어진 종합 지표이며, 서로 다른 두 Object Detection 모델의 성능을 정량적으로 비교하기 용이하기에 이를 활용하여 주로 Object Detection 모델의 성능을 평가합니다. AP에 대한 설명은 많은 부분 rafaelpadilla님의 github repository를 참고했습니다.


위의 예시를 보면 7장의 이미지에서 15개의 ground truth box(녹색 box)가 있으며, 24개의 bounding box(빨간색 box)가 있습니다. 각각의 bounding box는 알파벳을 통해 구분되며 confidence score를 가집니다. IoU 임계값이 0.3이라고 가정하면 왼쪽의 표와 같이 나타낼 수 있습니다.
예를 들어 몇 개의 bounding box를 살펴보도록 하겠습니다. Image 1의 bounding box A는 IoU 임계값이 0.3 미만이므로 FP에 해당합니다. B는 IoU가 임계값이 넘으므로 TP이며, C는 객체가 있다고 판별했지만 실제 객체가 위치하지 않았으므로 FP입니다.
만약 confidence score를 고려하지 않고(confidence score의 임계값이 0이라 가정한 경우) Precision 값을 구할 경우 위의 도표를 보면 TP=7, FP=17입니다. 이를 기반으로 볼 때 Precision(TP/FP+TP 혹은 TP/#predicted box)값은 7/24이며, Recall(TP/FN+TP 혹은 TP/#ground truth) 값은 7/15입니다. 하지만 AP 값을 구하기 위해선 confidence score 임계값 변화에 따른 모든 구간의 Precision과 Recall 값을 구해야 합니다.


PR 곡선을 그리기 위해서 먼저 위의 bounding box를 confidence score에 따라 내림차순으로 정렬합니다. 여기서 confidence score 임계값의 변화는 임의로 지정하는 것이 아니라 각 bounding box의 confidence score를 기준으로 하기 때문에 내림차순으로 나열했습니다. 위의 그래프를 보면 confidence score 변화에 따른 TP,FP의 누적값을 나타내는 TP Acc(Accumulated), FP Acc 컬럼이 있습니다. 누적된 값은 모델이 생성한 bounding box의 수, 즉 검출 수를 의미합니다. 이를 활용하여 각 confidence score 구간별로 Precision, Recall 값을 구할 수 있습니다.
- 위의 표에서 첫 번째 열에 위치한 R box의 경우 confidence score가 0.95일 경우로 TP가 나왔습니다. 이를 누적하여 보면 confidence score 임계값이 0.95일 때 한 번의 예측이 있었고 그 결과가 TP이므로 Precision은 1/1=1, Recall은 1/15=0.0666(15개의 ground truth 중 1번의 TP가 있었기 때문에)입니다.
- 두 번째 열에 위치한 Y box의 경우 FP이며 위에서부터 누적하면 2번의 예측 중 1번의 TP가 있었으므로 Precision은 1/2=0.5, Recall은 1/15=0.0666입니다.
- 바로 아래 열을 보면 confidence score의 임계값이 0.91일 경우로 J box는 TP이며 누적한 3번의 예측 중 TP=2, FP=1이므로 Precision=2/3=0.666, Recall은 2/15=0.1333입니다.
이와 같은 방식으로 모든 confidence score 임계값에 따른 Precision과 Recall값을 기록하여 그래프로 나타내면 오늘쪽 그래프와 같습니다. 다음으로 그래프의 PR 곡선 아래의 면적을 구하도록 하겠습니다.
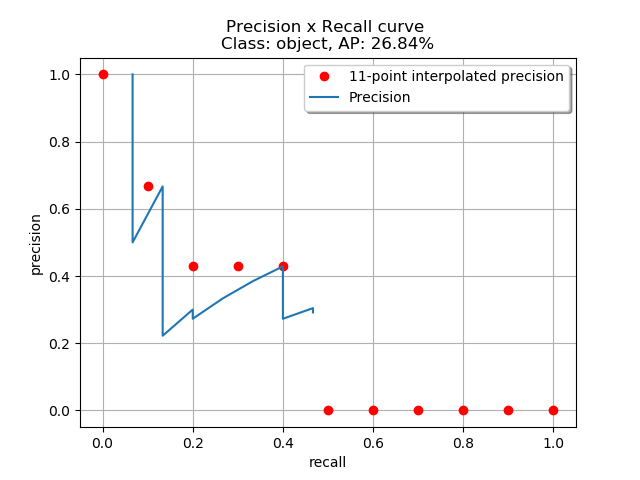
$$AP = {1\over11} \sum_{r \in \{0, 0.1, ..., 1 \}} \rho_ {interp(r)}$$
$$\rho_{interp} = \max_{\tilde{r}:\tilde{r} \ge r} \rho(\tilde{r})$$
$$AP = {1\over11}(1 + 0.6666 + 0.4285+ 0.4285 \\+ 0.4285 + 0 + 0 + 0 + 0 + 0 + 0) = 26.84$$
여기서 계산의 편의를 위해 11보간법(11-point interpolation)을 적용하여 PR 곡선의 면적을 구합니다. 11 보간법은 Recall값의 0.1 구간(0, 0.1, 0.2,...,1.0)마다 Precision 값을 구해 더한 후 평균을 구하는 방식입니다.
공식은 위와 같습니다. $\tilde{r}$은 Recall값을 의미하며, $\rho(\tilde{r})$은 Recall값이 $\tilde{r}$일때 Precision의 값을 의미합니다. $\rho_{interp}$는 Recall값이 같을 때 최댓값을 가짐을 의미합니다. R과 Y는 같은 Recall값을 가지나 Precision 값은 R이 더 높습니다. 이 경우 $\rho_{interp}$은 R의 Precision값이 됩니다. 11보간법을 적용하면 위의 예시의 AP값 26.84%입니다.
6) mAP(mean Average Precision)

AP는 단일 객체에 대한 모델의 검출 성능을 측정합니다. 예를 들어 자전거, 새, 비행기에 대한 객체를 검출하는 모델이 있다면 각 객체별로 AP값이 도출되는 셈입니다. 모든 객체에 대한 모델의 종합적인 검출 성능을 측정하기 위해 모든 AP값의 평균을 매긴 mAP(mean Average Precision)을 사용합니다. 위의 도표는 R-CNN 논문에서 발췌한 성능 평가표로 각 객체별(aero, bike, bird...)로 AP값을 가지고 이를 평균낼 mAP가 별도록 존재하는 것을 확인할 수 있습니다.
지금까지 Object Detection의 정의와 metric에 대해 살펴봤습니다. 객체의 범주를 예측하는 것을 넘어 위치 추정까지 더해지다보니 metric이 이해하기 어려웠습니다😂. 하지만 매번 헷갈렸던 Precision, Recall 개념을 제대로 이해했고, 앞으로 공부할 Object Detection 분야의 스타트를 끊을 수 있었던 좋은 기회였던 것 같습니다. Object detection metric을 python으로 구현한 코드는 Python으로 구현한 mAP(mean Average Precision) 포스팅을 참고하시기 바랍니다.
Reference
rafaelpadilla님의 github repository(metrics for object detection)
스카이비전님의 블로그(물체 검출 알고리즘 성능 평가방법 AP(Average Precision)의 이해)
다크 프로그래머님의 블로그(precision, recall의 이해)
cognithee님의 youtube 재생목록(Precision, Recall & Mean Average Precision for Object Detection)




