| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- IOU
- Faster R-CNN
- Bounding box regressor
- YOLO
- Fast R-CNN
- AP
- Detection Transformer
- mean Average Precision
- hard negative mining
- Multi-task loss
- herbwood
- Linear SVM
- RPN
- Map
- R-CNN
- Object Detection
- RoI pooling
- Object Detection metric
- fine tune AlexNet
- Anchor box
- multi task loss
- Hungarian algorithm
- object queries
- Average Precision
- pytorch
- Non maximum suppression
- BiFPN
- Region proposal Network
- detr
- Darknet
- Today
- Total
약초의 숲으로 놀러오세요
DETR 논문(End-to-End Object Detection with Transformers) 리뷰 본문
DETR 논문(End-to-End Object Detection with Transformers) 리뷰
herbwood 2023. 1. 6. 17:08이번에는 ECCV 2020년에 발표된 DETR 논문(End-to-End Object Detection with Transformers)을 읽고 리뷰해도록 하겠습니다. DETR은 Transformer 구조를 활용하여, end-to-end로 object detection을 수행하면서도 높은 성능을 보였습니다. 현재 많은 SOTA 모델들이 DETR을 기반으로 발전한만큼, 반드시 읽어야하는 기념비적인 논문이라고 할 수 있습니다.
Research gap
본 논문에서는 object detection을 bounding box와 category라는 set $G = \{(B_0, C_0), (B_1, C_1), …, (B_n, C_n)\}$을 예측하는 task로 정의합니다. 이 때 기존의 object detection 방법은 직접적으로 set을 예측하는 것이 아니라, 다수의 proposal, anchor, window center 등을 기반으로 set을 찾는 간접적인 방법에 기반을 두고 있습니다. 반면 본 논문에서는 이러한 pipeline을 간소화하기 위해 set을 직접적으로 예측하는 접근법을 제안합니다.

기존 object detection 방법론은 가진 pre-defined anchor를 사용합니다. 이미지 내 고정된 지점마다 다양한 scale, aspect ratio를 가진 anchor를 생성합니다. 이후 anchor를 기반으로 생성한 예측 bounding box와 ground truth를 match합니다. Matching 시, ground truth와의 IoU 값이 특정 threshold 이상일 경우 positive sample으로, 이하일 경우 negative sample로 간주하며, positive sample에 대해서만 bounding box regression을 수행합니다. 이처럼 threshold를 기준으로 독립적으로 prediction을 수행하기 때문에 하나의 ground truth에 다수의 bounding box가 matching됩니다. 이로 인해 예측한 bounding box와 ground truth의 관계가 many-to-one이 됩니다.
기존의 방법은 다수의 anchor를 생성함으로써, 다양한 크기와 형태의 객체를 효과적으로 포착하는 것이 가능합니다. 하지만 하나의 ground truth를 예측하는 다수의 bounding box가 존재하기 때문에, 이러한 near-duplicate한 예측, redundant한 예측을 제거하기 위해 NMS(Non Maximum Suppression)과 같은 post-processing 과정이 반드시 필요합니다. bounding box regression과 NMS에 대한 설명은 R-CNN 블로그 포스팅을 참고해주세요.

반면 DETR은 여러 크기의 직접 정의한 hand-crafted anchor를 사용하지 않습니다. 또한 하나의 ground truth에 오직 하나의 예측된 bounding box만 matching합니다. 이를 통해 예측한 bounding box와 ground truth의 관계가 one-to-one이 됩니다. 하나의 Ground truth를 예측하는 bounding box가 오직 하나이기 때문에 redundant한 bounding box가 없습니다. 따라서 post-processing 과정이 필요하지 않습니다.
Contribution
본 논문에서 주장하는 contribution은 다음과 같습니다.
- 본 논문에서는 object detection을 direct set prediction으로 정의하여, transformer와 bipartite matching loss를 사용한 DETR(DEtection TRansformer)을 제안합니다.
- DETR은 COCO dataset에 대하여 Faster R-CNN과 비슷한 수준의 성능을 보입니다.
- 추가적으로, self-attention을 통한 global information(전역 정보)를 활용함으로써 크기가 큰 객체를 Faster R-CNN보다 훨씬 잘 포착합니다.
Preliminaries
먼저 본 논문을 이해하기 위한 사전지식을 간략하게 살펴보도록 하겠습니다.
1. Hungarian algorithm
앞서 언급했듯이, DETR은 predicted bounding box와 ground truth를 일대일로 matching합니다. loss를 최소화할 수 있는 matching을 찾기 위해 가능한 모든 조합 경우의 수를 고려하는 brute force 방법을 사용하면 지나치게 많은 시간이 걸린다는 문제가 있습니다. 그래서 본 논문에서는 Hungarian algorithm을 사용합니다.
Hungarian algorithm은 두 집합 사이의 일대일 대응 시 가장 비용이 적게 드는 bipartite matching(이분 매칭)을 찾는 알고리즘입니다. Hungarian algorithm은 어떠한 집합 $I$와 matching 대상인 집합 $J$가 있으며, $i \in I$를 $j \in J$에 matching하는데 드는 비용을 $c(i, j)$라고 할 때, $\sigma : I \to J$로의 일대일 대응 중에서 가장 적은 cost가 드는 matching에 대한 permutation $\sigma$을 찾는 것입니다. 여기서 말하는 permutation은 matching 시 최적의 순서에 대한 index를 의미합니다. Hungarian algorithm은 $I, J$에 대한 cost를 표현한 행렬에 대하여 동작합니다. 구체적인 동작 과정은 Gazelle and Computer Science님의 블로그를 참고하시기 바랍니다.

DETR에서는 predicted bounding box를 ground truth에 일대일로 matching시키기 위해 Hungarian algorithm을 사용합니다. 위의 예시는 이미지 내 두 개의 객체(두 명의 사람)이 있을 때, predicted bounding box에서 ground truth를 matching하는 문제입니다. 이 때 cost에 대한 행렬을 Fig 3과 같이 표현할 수 있습니다. 행렬의 행은 predicted bounding box를, 열은 ground truth를 의미하며, 행렬의 각 요소는 predicted bounding box가 ground truth로 matching되었을 때의 cost를 의미합니다. 가령 1번 predicted bounding box가 2번 ground truth로 matching되었을 때의 cost는 11입니다. 지금처럼 permutation이 [1, 2, 3, 4, 5]인 경우, 즉 1번 bounding box가 1번 ground truth로 matching되고, 2번 bounding box가 2번 ground truth에 매칭되고...인 경우, cost가 32인 것을 확인할 수 있습니다.

반면 Fig 4와 같이 permutation을 [3, 4, 1, 5, 2]인 경우, cost가 12로 상대적으로 매우 낮으며 가장 바람직하게 matching된 것을 확인할 수 있습니다. Hungarian algorithm은 이처럼 cost에 대한 행렬을 입력 받아, matching cost가 최소인 permutation을 출력합니다.
2. Bounding box Loss
다음으로 Hungarian algorithm 연산 시, 그리고 loss 계산 시 사용되는 bounding box loss를 살펴보겠습니다. 기존의 방법들은 anchor를 기반으로 bounding box prediction을 수행하기 때문에 예측하는 bounding box의 범위가 크게 벗어나지 않습니다. 반면 DETR은 어떠한 initial guess가 없이 bounding box를 예측하기 때문에 예측하는 값의 범주가 상대적으로 큽니다. 따라서 절대적인 거리를 측정하는 l1 loss만을 사용할 경우, 상대적인 error는 비슷하지만 크기가 큰 box와 작은 box에 대하여 서로 다른 범위의 loss를 가지게 될 것입니다(큰 box는 큰 loss를, 작은 box는 작은 loss를). 이러한 문제를 해결하기 위해 본 논문에서는 l1 loss와 generalized IoU(GIoU) loss를 함께 사용합니다.

$GIoU = IoU(b_{\sigma(i)}, \hat{b}) - {{|B(b_{\sigma(i)}, \hat{b})| \backslash b_{\sigma(i)} \cup \hat{b_i}} \over {|B(b_{\sigma(i)}, \hat{b})|}}$
$\mathcal{L}_{iou}(b_{\sigma(i)}, \hat{b}) = 1 - GIoU$
generalized IoU(GIoU) loss는 두 box 사이의 IoU(Intersection over Union) 값을 활용한 loss로 scale-invariant하다는 특징이 있습니다. GIoU를 구하기 위해서는 predicted box $b_{\sigma(i)}$와 ground truth box $\hat{b_i}$를 둘러싸는 가장 작은 box $B(b_{\sigma(i)}, \hat{b})$를 구합니다. 이 때 predicted box와 ground truth box가 많이 겹칠수록 $B(b_{\sigma(i)}, \hat{b})$가 작아지며, 두 box가 멀어질수록 $B(b_{\sigma(i)}, \hat{b})$가 커집니다. $IoU(b_{\sigma(i)}, \hat{b})$는 두 box 사이의 IoU를 의미하며 ${|B(b_{\sigma(i)}, \hat{b})| \backslash b_{\sigma(i)} \cup \hat{b_i}} \over {|B(b_{\sigma(i)}, \hat{b})|}$는 $B(b_{\sigma(i)}, \hat{b})$에서 predicted box와 ground truth box를 합한 영역을 뺀 영역에 해당합니다. 이 때 $GIoU$는 -1~1 사이의 값을 가지며, GIoU를 loss로 사용할 때 $1 - GIoU$ 형태로 사용하여 loss의 최대값은 2, 최소값은 0이 됩니다. 보다 구체적인 설명은 JINSOL KIM님의 블로그를 참고하시기 바랍니다.
$\mathcal{L}_{box}(b_{\sigma(i)}, \hat{b}) = \lambda_{iou} \mathcal{L}_{iou}(b_{\sigma(i)}, \hat{b}) + \lambda_{L1} ||b_{\sigma(i)} - \hat{b}||_1$
l1 loss와 GIoU loss를 사용한 전체 bounding box loss는 위와 같습니다. 이 때 $\lambda_{iou}, \lambda_{L1}$은 두 term 사이를 조정하는 scalar hyperparameter입니다. 이 두 loss는 mini-batch 내 객체의 수에 따라 normalize됩니다.
3. Transformer for NLP task vs DETR Transformer
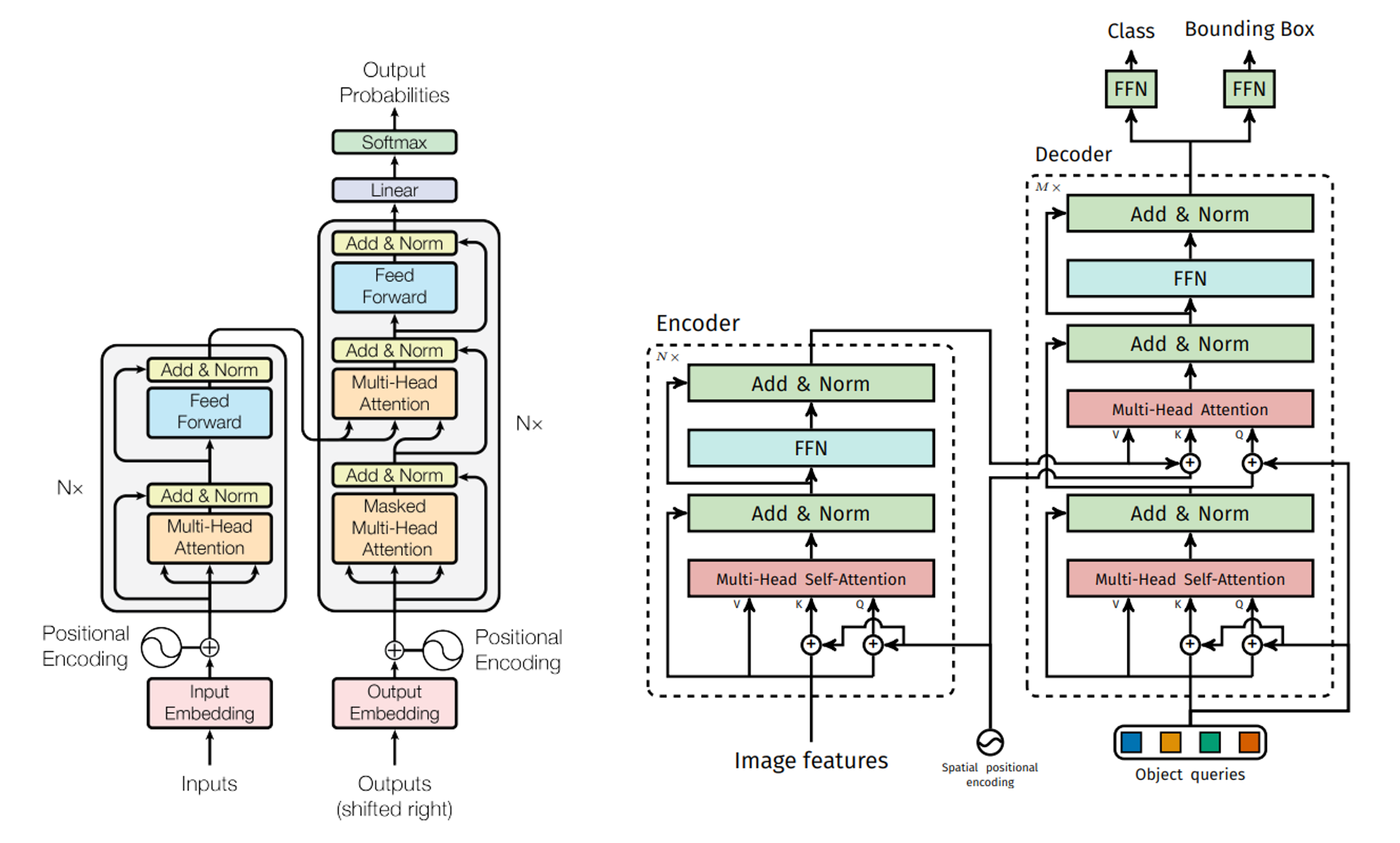
앞서 Hungarian algorithm 파트에서 살펴보았듯이 DETR은 반복되는 prediction을 제거하기 위해 object detection task를 prediction bounding box 집합과 ground truth box 집합을 matching하는 set prediction으로 정의합니다. DETR은 효과적인 matching을 위해 encoder-decoder 구조의 Transformer를 사용합니다. Transformer의 self-attention은 모든 입력 sequence의 token 사이의 상호작용(pairwise interaction)을 모델링하기 때문에 set prediction에 적합합니다. 하지만 DETR에서 사용하는 Transformer와 NLP task에서 사용하는 Transformer는 입출력 측면에서 다섯 가지 차이가 있습니다.
첫 번째로 DETR는 encoder에서 이미지 feature map을 입력받는 반면, Transformer는 문장에 대한 embedding을 입력받습니다. Transformer는 sequence 정보를 입력받는데 적합하기 때문에 DETR은 CNN backbone에서 feature map을 추출한 이후, 1x1 convolution layer를 거쳐 차원을 줄인 다음, spatial dimension을 flatten하여 encoder에 입력합니다. $h, w$가 height, width이며, $C$가 channel 수, $d$가 $C$보다 작은 channel 수라고 할 때 $C \times h \times w$ 크기의 feature map을 $d \times hw$로 변환시켰다고 볼 수 있습니다.
두 번째로 positional encoding에서 차이가 있습니다. Transformer는 입력 embedding의 순서와 상관 없이 동일한 값을 출력하는 permutation invariant한 성질을 가졌기 때문에 positional encoding을 더해줍니다. DETR은 x, y axis가 있는 2D 크기의 feature map을 입력받기 때문에 기존의 positional encoding을 2D 차원으로 일반화시켜 spatial positional encoding을 수행합니다. 입력값의 차원이 $d$라고 할 때 x, y 차원에 대하여, row-wise, column wise로 $2 \over d$ 크기로 sine, cosine 함수를 적용합니다. 이후 channel-wise하게 concat하여 $d$ channel의 spatial positional encoding을 얻은 후 입력값에 더해줍니다.
세 번째로, Transformer는 decoder에 target embedding을 입력하는 반면, DETR은 object queries를 입력합니다. object queries는 길이가 $N$인 학습 가능한 embedding입니다. object query에 대한 구체적인 설명은 Method 파트에서 살펴보겠습니다.
네 번째로, Transformer는 decoder에서 첫 번째 attention 연산 시 masked multi-head attention을 수행하는 반면, DETR은 multi-head self-attention을 수행합니다. 이는 Transformer는 auto-regressive하게 다음 token을 예측하기 때문에 attention 연산 시 다음 token에 대한 정보를 활용하는 것을 방지하기 위해 후속 token에 대한 정보를 masking합니다. masking은 attention 연산에서 softmax 함수 입력에 후속 token 위치에 -inf를 입력하는 방식으로 수행됩니다. 하지만 DETR은 입력된 이미지에 동시에 모든 객체의 위치를 예측하기 때문에 별도의 masking 과정을 필요로 하지 않습니다.
마지막으로 Transformer는 Decoder 이후 하나의 head를 가지는 반면, DETR는 두 개의 head를 가집니다. Transformer는 다음 token에 대한 class probability를 예측하기 때문에 하나의 linear layer를 가지는 반면, DETR은 이미지 내 객체의 bounding box와 class probability를 예측하기 때문에 각각을 예측하는 두 개의 linear layer를 가집니다.
Method
본 논문에서는 object detection 시 direct set prediction을 위해 두 가지 요소가 필수적이라고 합니다.
(1) predicted bounding box와 ground truth box 사이의 unique matching을 가능하도록 하는 set prediction loss
(2) 한 번의 forward pass로 object model 사이의 relation을 예측하는 architecture
1. Object detection set prediction loss

먼저 첫 번째 조건 (1)을 충족하기 위해 loss를 계산하는 과정은 두 단계로 구분됩니다. 첫 번째로, predicted bounding box와 ground truth box 사이의 unique한 matching을 수행하는 과정입니다. 두 번째 단계에서는 matching된 결과를 기반으로 hungarian loss를 연산합니다. 이 중 먼저 첫 번째 단계부터 살펴보겠습니다.
1.1 Find optimal matching
기존의 연구는 수 천개의 anchor를 생성하여, 객체를 예측하기 위한 proposal로 사용하는데 이는 객체가 “얼마나” 있는지 알 수 없기 때문입니다. 본 논문에서 제안한 DETR은 고정된 크기의 $N$개의 prediction만을 수행함으로써, 수많은 anchor를 생성하는 과정을 우회합니다. 이 때 $N$은 일반적으로 이미지 내 존재하는 객체의 수보다 훨씬 더 큰 수로 지정했습니다. 즉, 이는 DETR을 통해 예측하는 객체의 수는 최대 $N$개임을 의미합니다. 이를 통해 적은 수의 prediction이 생성되어, ground truth와의 unique matching을 상대적으로 쉽게 수행할 수 있습니다.
$y$는 객체에 대한 ground truth set이며 $\hat{y}$은 $N$개의 prediction입니다. 이 때 $y$의 크기 역시 $N$개이며, 객체의 수를 제외한 나머지는 $\varnothing$ (no object)로 pad됩니다. 즉 이미지 내 객체의 수가 3개이면, $y$에서 97개는 $\varnothing$ 로 pad됩니다. 이 때 두 개의 set에 대하여 bipartite matching을 수행하기 위해, 아래의 cost를 minimize할 수 있는 $N$의 permutation을 탐색합니다.
$\hat{\sigma} = argmin_{\sigma \in \mathfrak{S}_N} \sum_i^N \mathcal{L}_{match}(y_i, \hat{y}_\sigma(i))$
이 때 $\mathcal{L}_{match}(y_i, \hat{y}_\sigma(i))$ 는 ground truth $y_i$와 index가 $$인 prediction 사이의 pair-wise matching cost입니다. 이러한 matching cost는 class prediction과 predicted bounding box와 ground truth box 사이의 similarity(유사도)를 모두 고려합니다. ground truth의 $i$번째 요소인 $y_i=(c_i, b_i)$이며, 이 때 $c_i$는 target class label을 의미하며, $b_i \in [0, 1]^4$는 ground truth box의 좌표와 이미지 크기에 상대적인 width, height를 의미합니다. 이 때 $c_i$는 $\varnothing$ 가 될 수 있습니다. index가 $\sigma(i)$인 prediction 결과에 대해 class probability를 $\hat{p}_{\sigma(i)}(c_i)$로, predicted box를 $\hat{b}_{\sigma(i)}$로 정의합니다. 이 때 matching cost를 다음과 같이 표현할 수 있습니다.
$\mathcal{L}_{match} = -\mathbb{1}_{\{c_i \ne \varnothing\}} \hat{p}_{\sigma(i)}(c_i) + \mathbb{1}_{\{c_i \ne \varnothing \}} \mathcal{L}_{box} (b_i, \hat{b}_{\sigma(i)})$
이 때 $\mathcal{L}_{box}$는 Preliminaries에서 언급한 bounding box loss입니다.

predicted bounding box와 ground truth box에 대한 matching cost 행렬은 위와 같이 표현할 수 있습니다. 이러한 최적의 assignment는 Hungarian algorithm에 의해 효율적으로 연산됩니다. 이와 같은 matching 과정은 기존의 heuristic한 방법과 비슷한 역할을 수행합니다. 하지만 duplicate, 즉 같은 ground truth를 예측하는 여러 prediction 없이, direct로 set을 예측하기 위해 one-to-one matching을 찾아야한다는 점에서 차이가 있습니다.
1.2 Compute Hungarian loss
앞선 과정을 통해 matching된 pair를 기반으로 loss function인 Hungarian loss를 계산합니다. 이 때 loss는 class loss와 box loss로 구성됩니다. class loss는 prediction에 대한 negative log-likelihood를 구합니다. box loss는 Preliminaries에서 언급했듯이 l1 loss와 generalized IoU loss를 결합하여 사용합니다.
$\mathcal{L}_{Hungarian}(y, \hat{y}) = \sum_{i=1}^N [-log \hat{p}_{\hat{\sigma}(i)}(c_i) + \mathbb{1}_{\{c_i \ne \varnothing \}} \mathcal{L}_{box}(b_i, \hat{b}_{\hat{\sigma}}(i))] $
$\hat{\sigma}(i)$는 이전 단계에서 구한 optimal assignment입니다. 실제 학습 시 예측하는 객체가 없는 경우인 $c_i = \varnothing$에 대하여 log-probability를 1/10로 down-weight한다고 합니다. 이는 실제로 객체를 예측하지 않는 negative sample의 수가 매우 많아 class imbalance를 위해 해당 sample에 대한 영향을 감소시키기 위함입니다.
2. DETR architecture

DETR은 1) CNN backbone 2) Transformer encoder와 decoder 3) FFN(Feed Forward Network)로 구성되어 있습니다.
2.1 Backbone
먼저 입력 이미지 $x_{img} \in \mathbb{R}^{3 \times H_0 \times W_0}$를 CNN backbone network에 입력하여, feature map $f \in \mathbb{R}^{C \times H \times W}$를 생성합니다. 이 때 $C=2048$이며, $H, W = {H_0 \over 32}, {W_0 \over 32}$입니다.
2.2 Transformer encoder
이후 1x1 convolution 연산을 적용하여, $C$차원의 feature map을 $d$ 차원으로 감소시켜 새로운 feature map $z_0 \in \mathbb{R}^{d \times H \times W}$을 생성합니다. Transformer encoder는 sequence를 입력으로 받기 때문에 $z_0$의 spatial dimension을 collapse(=flatten)하여 크기를 $d \times HW$로 변경시켜줍니다. 각 encoder layer는 multi-head self-atttention module과 feed forward network(FFN)으로 구성되어 있습니다. Transformer 구조는 입력 embedding의 순서와 상관없이 같은 출력값을 생성하는 permutation-invariant 속성이 있기 때문에 encoder layer 입력 전에 입력 embedding에 positional encoding을 더해줍니다.
2.3 Transformer decoder
Transformer decoder는 masking을 통해 다음 token을 예측하는 autoregressive 방법을 사용하는 반면, DETR의 decoder는 $N$개의 object에 대한 정보를 한번에 출력합니다. Decoder 역시 permutation-invariant하기 때문에 입력으로 받는 embedding으로 object queries라고 불리는 learnt positional encoding을 사용합니다.
object query는 object query feature과 object query positional embedding으로 구성되어 있습니다. object query feature는 decoder에 initial input으로 사용되어, decoder layer를 거치면서 학습됩니다. query positional embedding은 decoder layer에서 attention 연산 시 모든 query feature에 더해집니다. query feature는 학습 시작 시 0으로 초기화(zero-initialized)되며, query positional embedding은 학습 가능(learnable)합니다. 이러한 object queries는 길이가 $N$으로, decoder에 의해 output embedding으로 변환(transform)되며 이후 FFN을 통해 각각 독립적으로(independently) box coordinate와 class label로 decode됩니다. 이는 각각의 object query는 하나의 객체를 예측하는 region proposal에 대응된다고 볼 수 있습니다. 즉, object queries는 $N$개의 객체를 예측하기 위한 일종의 prior knowledge로도 볼 수 있습니다. object query에 대한 설명은 Mask2Former 논문을 참고했습니다.
encoder와 유사하게 object query를 각 attention layer의 입력에 더해줍니다. 이 때 embedding은 self-attention과 encoder-decoder attention을 통해 이미지 내 전체 context에 대한 정보를 사용합니다. 이를 통해 객체 사이의 pair-wise relation을 포착하여 객체간의 전역적(global)인 정보를 모델링하는 것이 가능해집니다.
2.4 Prediction feed-forward networks(FFNs)
Decoder에서 출력한 output embedding을 3개의 linear layer와 ReLU activation function으로 구성된 FFN에 입력하여 최종 예측을 수행합니다. FFN은 이미지에 대한 class label과 bounding box에 좌표(normalized center coordinate, width, height)를 예측합니다. 이 때 예측하는 class label 중 $\varnothing$은 객체가 포착되지 않은 경우로, "background" class를 의미합니다.
2.5 Auxiliary decoding losses
학습 시, 각 decoder layer마다 FFN을 추가하여 auxiliary loss를 구합니다. 이러한 보조적인 loss를 사용할 경우 모델이 각 class별로 올바른 수의 객체를 예측하도록 학습시키는데 도움을 준다고 합니다. 추가한 FFN은 서로 파라미터를 공유하며, FFN 입력 전에 사용하는 layer normalization layer도 공유합니다.
Overall training procedure
전체 학습 과정을 순서대로 살펴보자면 다음과 같습니다.
1) Extract feature map by CNN backbone

이미지 $x_{img} \in \mathbb{R}^{3 \times H \times W}$를 CNN backbone인 ResNet에 입력하여 feature map $f \in \mathbb{R}^{C \times h \times w}$ 추출합니다. $C$는 channel 수, $H, W$는 원본 이미지의 height, width, $h, w$는 feature map의 height, width입니다.
- Input : image $x_{img} \in \mathbb{R}^{3 \times H \times W}$
- Output : feature map $f \in \mathbb{R}^{C \times h \times w}$
2) Add Positional Encoding

feature map $f$을 1x1 convolution layer에 입력한 후 spatial dimension을 collapse해줍니다. flatten된 feature map $z_0 \in \mathbb{R}^{d \times hw}$에 대한 spatial positional encoding을 구합니다.
- feature map과 동일한 해상도의 mask $m \in \mathbb{R}^{1 \times h \times w}$에 대하여 y축 방향으로(row-wise) 누적합을 구해줍니다. 여기서 mask는 이미지가 존재하는 영역은 1, 존재하지 않는 영역은 0으로 표시한 binary mask입니다. mask에 대한 누적합을 구함으로써 y축에 대한 절대적인 위치를 구할 수 있습니다.
- Transformer의 positional encoding과 같이 각 위치에 대한 sin, cos 변환을 수행합니다.
- 동일하게 mask에 대하여 x축 방향으로(column-wise) 누적합을 구한 후 앞서 동일한 과정을 거칩니다.
- x, y축에 대한 positional encoding을 concat하여 feature map과 동일한 차원의 spatial positional encoding $P \in \mathbb{R}^{d \times h \times w}$을 구해줍니다.
spatial positional encoding은 Encoder의 모든 multi-head self-attention layer에서 query와 key에 더해집니다.
- Input : feature map $f \in \mathbb{R}^{C \times h \times w}$
- Output : feature map $z_0 \in \mathbb{R}^{d \times hw}$, positional encoding $P \in \mathbb{R}^{d \times hw}$
3) Generate Object queries
query feature $q_f \in \mathbb{R}^{N \times d}$와 query positional embedding $q_p \in \mathbb{R}^{N \times d}$를 생성합니다. 이 때 $N$은 prediction의 수이며, $d$는 channel의 수입니다. query feature는 zero initialize됩니다. 이후 query feature와 query positional embedding을 더해 object query $q \in \mathbb{R}^{N \times d}$를 생성합니다. query positional embedding은 Decoder의 모든 multi-head self-attention layer에서 query와 key에 더해집니다.
- Input : query feature $q_f \in \mathbb{R}^{N \times d}$, query positional embedding $q_p \in \mathbb{R}^{N \times d}$
- Output : object query $q \in \mathbb{R}^{N \times d}$
4) Output encoder memory by Transformer encoder

Encoder는 feature map $z_0$을 입력받아 multi-head self-attention, feed forward network를 거쳐 feature map에 대한 representation을 학습한 encoder memory $o_e \in \mathbb{R}^{hw \times d}$를 출력합니다. encoder memory는 모든 decoder의 multi-head attention layer에 전달됩니다.
- Input : feature map $z_0 \in \mathbb{R}^{d \times hw}$, positional encoding $P \in \mathbb{R}^{d \times hw}$
- Output : encoder memory $o_e \in \mathbb{R}^{hw \times d}$
5) Output output embedding by Transformer decoder
Decoder는 object queries $q$를 입력받아 multi-head self attention layer를 거친 후, encoder memory $o_e$와 multi-head attention을 수행합니다. 이후 feed forward network를 거쳐 output embedding $o_d \in \mathbb{R}^{hw \times d}$을 출력합니다.
- Input : object queries $q \in \mathbb{R}^{N \times d}$, encoder output embedding $o_e \in \mathbb{R}^{hw \times d}$
- Output : output embedding $o_d \in \mathbb{R}^{hw \times d}$
6) Class prediction by Class head
Class prediction head는 Decoder의 output embedding $o_d$를 입력받아, fully connected layer를 통해 $N$개의 prediction에 대한 class prob $p(c) \in \mathbb{R}^{N \times (c+1)}$를 출력합니다. class의 수가 $c$라고 할 때 배경까지 고려하여 $c+1$개의 class를 예측합니다.
- Input : output embedding $o_d \in \mathbb{R}^{hw \times d}$
- Output : class prob $p(c_i) \in \mathbb{R}^{N \times (c+1)}$
7) Bounding box prediction by Bounding box head
Bounding box head는 Decoder의 output embedding $o_d$를 입력받아 fully connected layer를 통해 $N$개의 prediction에 대한 bounding box coordinate $\hat{b} \in \mathbb{R}^{N \times 4}$를 출력합니다.
- Input : output embedding $o_d \in \mathbb{R}^{hw \times d}$
- Output : bounding box coordinates $\hat{b} \in \mathbb{R}^{N \times 4}$
8) Match prediction with ground truth by Hungarian Matcher
$\mathcal{L}_{match} = -\mathbb{1}_{\{c_i \ne \varnothing\}} \hat{p}_{\sigma(i)}(c_i) + \mathbb{1}_{\{c_i \ne \varnothing \}} \mathcal{L}_{box} (b_i, \hat{b}_{\sigma(i)})$
class head와 bounding box head를 통해 $N$개의 class prob와 bounding box를 예측했습니다. 이를 기반으로 matching cost matrix를 활용하여 Hungarian matcher를 통해 prediction과 ground truth 사이의 matching cost를 최소화할 수 있는 최적의 permutation $\sigma(i)$을 탐색합니다.
- Input : class prob $p(c_i) \in \mathbb{R}^{N \times (c+1)}$, bounding box coordinates $\hat{b} \in \mathbb{R}^{N \times 4}$
- Output : permutation $\sigma(i)$
9) Compute losses
$\mathcal{L}_{Hungarian}(y, \hat{y}) = \sum_{i=1}^N [-log \hat{p}_{\hat{\sigma}(i)}(c_i) + \mathbb{1}_{\{c_i \ne \varnothing \}} \mathcal{L}_{box}(b_i, \hat{b}_{\hat{\sigma}}(i))] $
Hungarian matcher를 통해 구한 permutation $\sigma(i)$으로 matching된 prediction과 ground truth 사이의 loss를 구합니다. 이 때 matching된 class probability는 $\hat{p}_{\hat{\sigma}(i)}(c_i)$, bounding box는 $\hat{b}_{\hat{\sigma}}(i)$입니다.
- Input : class prob $p(c_i) \in \mathbb{R}^{N \times (c+1)}$, bounding box coordinates $\hat{b} \in \mathbb{R}^{N \times 4}$, permutation $\sigma(i)$
- Output : total loss $\mathcal{L}_{Hungarian}(y, \hat{y})$
Experiments
본 논문의 실험 결과를 정리했습니다. 제가 개인적으로 흥미롭게 본 실험은 빨간색 글씨로 표시했습니다.
Comparison with Faster R-CNN
- COCO dataset에 대한 실험 결과, DETR은 같은 수의 파라미터로 Faster R-CNN과 비슷한 수준의 성능을 보였습니다.
Ablations

- Number of encoder layers Encoder 수로 ablation study를 진행한 결과 encoder를 전혀 사용하지 않으면 성능이 3.9%p 감소했습니다. 저자들은 encoder가 global scene reasoning을 통해 객체를 분리하는 작업을 수행하기 때문이라고 가정합니다. 이는 encoder layer의 attention map을 시각화한 Fig 13을 통해 알 수 있습니다.

- Number of decoder layers decoder를 추가할수록 성능이 향상되었으며, 첫 번째와 마지막 decoder 사이에는 +8.2/9.5 AP 차이가 있었습니다. 하나의 decoder만을 사용한 경우 output에 대한 cross-correlation을 연산하지 못하기 때문에 duplicate prediction이 발생하였습니다. decoder의 attention map을 시각화한 결과, Fig 14과 같이 다소 local하게 객체를 포착하고 있습니다. 저자들은 encoder가 global attention을 통해 객체를 배경으로부터 분리했기 때문에 decoder는 객체의 경계 부분만 포착하면 될 것이라고 가정합니다.
- Importance of FFN Transformer에서 FFN을 제거하고 attention layer만 사용한 경우, AP 값이 2.3%p 감소했습니다.

- Importance of positional encoding spatial positional encoding을 사용하지 않고 decoder에 object queries만 사용한 결과 베이스라인에 비해 AP 값이 7.8%p 감소했습니다. 또한 decoder에 단 한 번 object query를 입력한 결과 모든 attention layer마다 object query를 더해주었을 때에 비해 AP 값이 1.4%p 감소했습니다.
- Loss ablations l1 loss와 GIoU loss에 대한 ablation 실험을 수행한 결과, GIoU loss만 사용한 경우 성능이 0.8%p 정도만 감소했으나, l1 loss만 사용한 경우 성능이 5%p 가까이 감소하였습니다. 이를 통해 GIoU loss가 사실상 bounding box loss에 대한 기여도가 매우 높음을 알 수 있습니다.
Analysis

- Decoder output slot analysis 각 object query의 slot에 대한 분석을 진행한 결과 각 slot은 여러 모드로 특정 영역과 box 크기의 객체를 학습하는데 특화된 모습을 보였습니다. Fig 16 은 20개의 slot에 대한 시각화 결과로, 각 점은 예측한 bounding box의 center coordinate을 의미합니다. 초록색은 작은 box, 빨간색은 큰 수평 box, 파란색은 큰 수직 box에 해당합니다. 또한 거의 모든 slot이 COCO dataset에서 자주 등장하는 입력 이미지와 비슷한 크기의 box를 예측하는 모드를 가지고 있습니다.

- Generalization to unseen numbers of instances 몇몇 class는 이미지 내 instance가 충분히 등장하지 않는 경우가 있습니다. 가령 COCO dataset에서 기린(giraff)가 13마리 이상 등장하는 이미지가 없습니다. 학습 데이터셋에 없는 수의 instance에 대한 실험을 진행하기 위해 Fig 17와 같이 synthetic image(가상 이미지)를 생성하여 실험한 결과 이미지 내 등장하는 24마리의 기린(out-of-distribution)을 모두 잘 포착하였습니다. 이를 통해 각 object query에는 강력한 class-specialization이 없음을 확인하였습니다.
DETR for panoptic segmentation

- DETR은 panoptic segmentation task에도 확장 가능함을 보였습니다. panoptic segmentation은 semantic- instance segmentation을 결합한 task입니다. 해당 task에서는 셀 수 있는 객체(차, 사람 등)을 Thing class, 셀 수 없는 객체(하늘, 길 등)을 Stuff class라고 합니다. Thing class에 대해서는 instance segmentation을, Stuff class에 대해서는 semantic segmentation을 수행합니다. panoptic segmentation에 대한 설명은 두더지 개발자 님의 블로그를 참고했습니다.
- Decoder output에 mask를 예측하는 head를 추가함으로써 segmentation을 수행할 수 있습니다. 실험 결과 기존의 연구와 비슷한 수준의 성능을 보였습니다. 특히 DETR은 Stuff class에 대하여 좋은 결과를 보였습니다. 저자들인 encoder attention에서 학습한 global reasoning 덕분이었다고 가정합니다.
Conclusion
DETR은 object detection을 set prediction task로 정의하여 prediction과 ground truth 사이의 일대일 matching을 수행했습니다. 이를 통해 near duplicate prediction을 효과적으로 감소시켜 post-processing 과정이 없는 end-to-end 프레임워크를 제안하였습니다. 이 과정에서 encoder-decoder 구조의 Transformer를 활용함으로써 입력 token 사이의 pairwise interaction과 global reasoning을 통해 준수한 성능을 보였습니다.
하지만 본 논문에서 제안한 방법도 단점이 있다고 할 수 있습니다. 여러 크기의 anchor를 사용하지 않기 때문에 다양한 크기, 형태의 객체를 포착하지 못합니다. 또한 하나의 예측 bounding box를 ground truth에 matching하기 때문에 converge하는데 훨씬 긴 학습시간을 필요로 합니다. 그럼에도 불구하고, 본 논문에서 제안한 DETR은 Faster R-CNN과 비슷한 성능을 보이면서도 heuristic한 과정이나 post-processing을 필요하지 않다는 점에서 큰 의의를 가진다고 할 수 있습니다.

References
DETR 논문(End-to-End Object Detection with Transformers)
Gazelle and Computer Science님의 블로그
Transformer 논문(Attention is all you need)




